Homework 2 Solution

Problem 1: Consider sending a 2400-byte datagram into a link that has an MTU of 700 bytes. Suppose the original datagram is stamped with the identification number 422. How many fragments are generated? What are the values in the various fields in the IP datagram(s) generated related to fragmentation?

Problem 2: (a) Consider a router that interconnects three subnets: Subnet 1, Subnet 2, and Subnet

1. Suppose all of the interfaces in each of these three subnets are required to have the prefix 223.1.17/24. Also suppose that Subnet 1 is required to support up to 63 interfaces, Subnet 2 is to support up to 95 interfaces, and Subnet 3 is to support up to 16 interfaces. Provide three network addresses (of the form a.b.c.d/x) that satisfy these constraints. (b) Consider a subnet with prefix 128.119.40.128/26. Give an example of one IP address (of form xxx.xxx.xxx.xxx) that can be assigned to this network. Suppose an ISP owns the block of addresses of the form 128.119.40.64/26. Suppose it wants to create four subnets from this block, with each block having the same number of IP addresses. What are the prefixes (of form a.b.c.d/x) for the four subnets?

Problem 3: Consider the wireless topology below. The solid circles represent the transmission radius of nodes A and D, respectively, and the dashed circles represent the transmission range of B and C, respectively. In these problems, assume that losses only occur due to collisions. list the potential hidden terminals and exposed terminals when

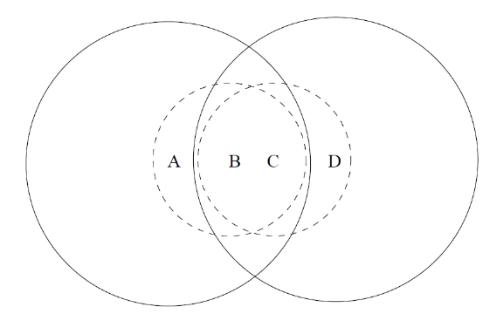
1. A is transmitting to B

1. B is transmitting to A

1. A is transmitting to C

1. D is transmitting to B

Problem 4: Consider a fully connected three-node topology. Let the link costs be c(x,y) = 4, c(y,z)

• 7, c(z,x) = 2. Compute the distance tables after the initialization step and after each iteration of distance-vector algorithm as done for the example in the lecture slides.