CS/ECE/ISyE 524 Homework 6: Least Squares

    1. Spline tting. We are running a series of experiments to evaluate the properties of a new uorescent material. As we vary the intensity of the incident light, the material should uoresce di erent amounts. Unfortunately, the material isn’t perfectly uniform and our method for measuring uorescence is not very accurate. After testing 200 di erent intensities, we obtained the result below (also available in xy_data.csv). The intensities xi and uorescences yi are recorded in the rst and second columns of the data matrix, respectively.




fluorescence

1.0 


0.8

0.6

0.4

0.2

0.0 

0    1    2    3    4    5    6    7    8    9    10

light intensity

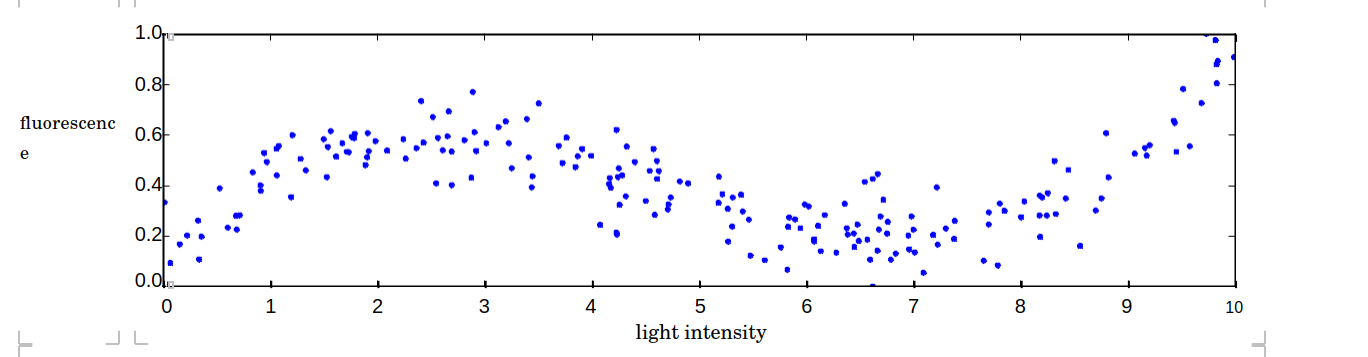
The material has interesting nonlinear properties, and we would like to characterize the relationship between intensity and uorescence by using an approximate model that agrees well with the trend of our experimental data. Although there is noise in the data, we know from physics that the uorescence must be zero when the intensity is zero. This fact must be re ected in all of our models!

    a) [3 points] Polynomial t. Find the best cubic polynomial t to the data. In other words, look for a function of the form y = a1x3 + a2x2 + a3x + a4 that has the best possible agreement with the data. Remember that the model should have (exactly) zero uorescence when the intensity is zero! Include a plot of the data along with your best- t cubic on the same axes.

    b) [3 points] Spline t. Instead of using a single cubic polynomial, we will look for a t to the data using two quadratic polynomials. Speci cally, we want to nd coe cients pi and qi so that our data is well modeled by the piecewise quadratic function:
y =
(q1x2
+ q2x + q3
if 4
x < 10

p1x2
+ p2x + p3
if 0
x < 4


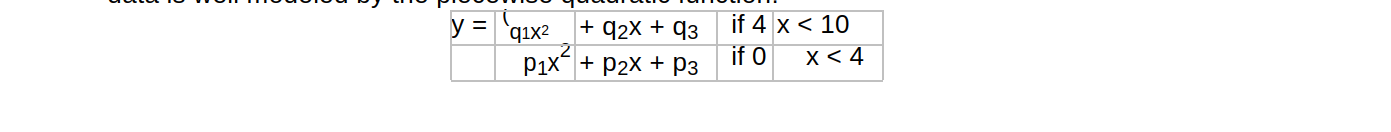
These quadratic functions must be designed so that:

as in the cubic model, there is zero uorescence when the intensity is zero. both quadratic pieces have the same value at x = 4.

both quadratic pieces have the same slope at x = 4.

In other words, we are looking for a smooth piecewise quadratic. This is also known as a spline (this is just one type of spline, there are many other types). Include a plot of the data along with your best- t model.









1 of 2
CS/ECE/ISyE 524    Introduction to Optimization    L. Roald,    Spring 2022


    2. [3 points] Voltage smoothing. We would like to send a sequence of voltage inputs to the manipulator arm of a robot. The desired signal is shown in the plot below (also available in voltages.csv).





voltage

2

1

0


−1

−2


0    50    100    150    200

time

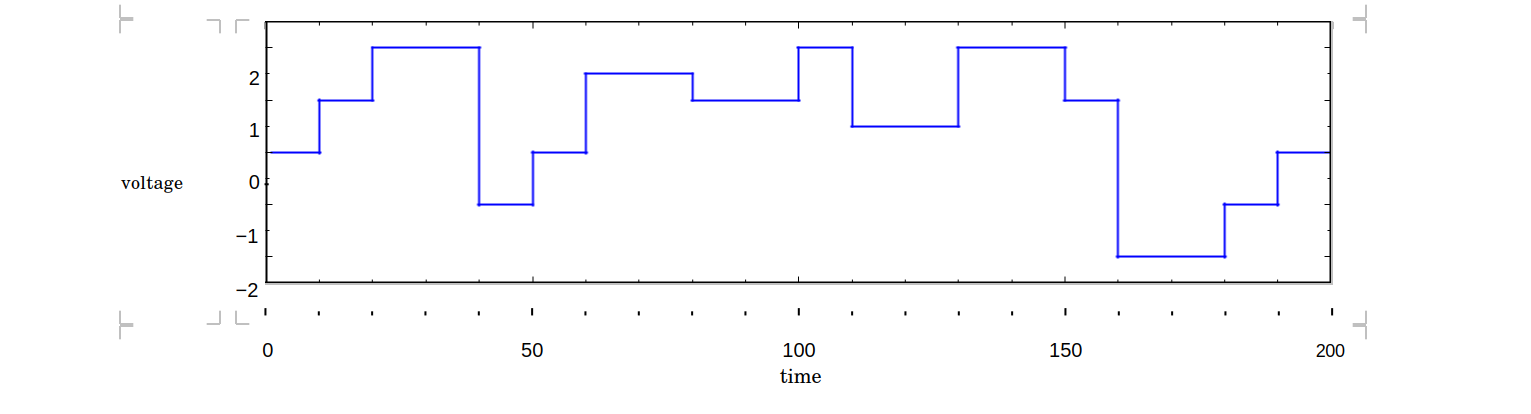
Unfortunately, abrupt changes in voltage cause undue wear and tear on the motors over time, so we would like to create a new signal that is similar to the one above but with smoother transitions. If the voltages above are given by v1; v2; : : : ; v200, one way to characterize smoothness is via the sum of squared di erences:
R(v) = (v2    v1)2 + (v3    v2)2 +    + (v200    v199)2

When R(v) is smaller, the voltage is smoother. Solve a regularized least squares problem that explores the tradeo between matching the desired signal perfectly and making the signal smooth. Include a plot comparing the original signal to a few di erent smoothed versions obtained using regularized least squares and with varying degrees of smoothness.